数学デーinあじうー結婚式二次会
この記事は数学デーアドベントカレンダーの21日目の記事です。
先日、数学デーin結婚式二次会に参加してきました!
服も脱ぎかけで今日の #数学デーin二次会 のアウトプットに浸る旦那さん pic.twitter.com/D27WM1vhZN
— ひらうー🍟 (@potatonokeshin) 2019年11月23日
まずは、ひらうーさん、鯵坂さんご結婚おめでとうございます☆
いや〜〜〜結婚式二次会楽しかった…!数学好きじゃない人もいたようなのですが、二人+司会のタカタ先生の掛け合いが面白くて盛り上がりましたね。これからも末永くお幸せに…!
さて、この結婚式は数学デーの主催者の方の結婚式の二次会でして、なんとテーブルに模造紙とペンが置いてあって「ご自由に議論してください」となっていました。
数学デーってなんだ??と思われた方には、なんと gendai にも紹介記事があるのでご紹介します。
数学を楽しむ感動を誰かと共有できる、部室に集まる学生のようなノリで楽しむイベント、とのこと。
私もしばらく行けていなかったのですが、今回結婚式二次会で久々に体験してみて、思いました。
手元に模造紙があるってめっっっっっっっっっっっっちゃくちゃいいですね。 視界が広いのでストレスなく書きまくれるし、担当者がはっきり決まったセミナーじゃないからみんな対等に向き合えるし気軽に数学の話ができる。だからといって楽をしているというわけでもなくて、その場で即興でしゃべって書くのでむしろ勉強不足なところも(話す人は)すごく良くわかります。あれ、ここ分かってなかったな、ここもうちょっとやりたいな、とか。それで、聞いてくれる人もすごく質問しやすい距離感なので、話が弾むんですよ!!!ここ分からなかった〜って言いやすいし、模造紙があるから話を広げやすい!!つじもったーさんが[tex: ii]の話に熱中しているのにつられて私も話が盛り上がりすぎちゃって、最初に書いていたドーナツの絵の上にまで書きなぐってしまいました…。それくらい話に熱中してしまった。アウトプットを気軽な頻度で楽しい雰囲気の中でできるってとてもいいなぁ〜と思いました!

繰り返し思い出して書くというのは記憶の定着に良いらしいのですが*1、でも数学のセミナーって厳しい指摘が飛んでくるイメージがあってなかなかやりにくい…って思う人も少なくないんじゃないかなと思います。私もセミナー後に辛くて泣いたことは数知れず…。部活みたいな雰囲気の中で、「へぇ〜面白い〜!」「これはどうなってるの??」「こういうのはどうかな??」ってポジティブな反応をもらいながら自分の考えていることを人に聞いてもらえて相談もできるって本当に実りが多いなと思います。数学デーはいま日本のあちこちで開催されているようで、大きな広がりを見せていますが、うーんそれも納得!普段の数学デーもぜひ行きたいです。
数学デー、気になる方はぜひ行ってみてください!!!!&ご自分の街でもやってみては??
さて、私がその日お話したのは Hesse 行列 (Hessian matrix) の話でした。今回ここでまとめて書こうかと思ったのですが、投稿日を23日だと勘違いしておりまして…。土日はセミナー3本ノックがあるので、改めて書こうかなと思います。
明日は grand_antiprism さんによる高次元の図形の切り口の話だそうです。お楽しみに〜。
追伸:数学デー主催者の鯵坂もっちょさんのブログも面白いのでぜひ読んでみてください!!初めての人にも伝えるのってとても難しいことだと思うのですが、鯵坂さんはいつも内容をよく理解した上で本質的なところを身近な例でわかりやすく話してくれて、とっても勉強になります。
結婚式→Riesz の表現定理→bra-ket 記法
この記事は、「日曜数学Advent Calendar 2019」の16日目の記事です。
昨日15日の記事は、onewan さんによる統計検定で学ぶ線形代数でした。
onewan さんは社会人としてバリバリ活躍されながら、いつも私がやっている数学カフェにも来て勉強していてとても励みになります。この間のSkypeセミナーは、なんと大阪への新幹線移動しながら参加していました!来年もよろしくお願いします。
さてそれでは日曜数学アドベントカレンダー16日目の記事です。勉強中の内容なので、ご指摘あればぜひお願いします!
はじめに
(すみません、texが上手くコンパイルされていないのですがちょっと今時間がないので後ほど直します…わかりにくくて本当にごめんなさい。。。)
ちょうど一ヶ月前の11/16に結婚披露宴をしました。夫と相談の上、2人の思い出といえば関数解析だよね、ということでウェディングケーキに関数解析の重要な定理の一つである Riesz の表現定理を描いて頂きました。2人の初めての共同作業といったらケーキカットより2人で定理の証明だろう!私単射性示すから、あなたは全射性をお願い!みたいなやつ…と思っていたのですが、ちょっとアバンギャルドすぎるし、万一の炎上が怖くて安定した古典的な方法を採用しました。どなたか、ぜひやってみてください。
そしてその披露宴のケーキの写真がこちら。
控えめに言って最高にフォトジェニックでインスタ映えする Riesz の表現定理が描かれたウェディングケーキがこちらになります pic.twitter.com/FPLvBJ9f7f
— H. Hosaka (@H_H) 2019年11月16日
ちょ、バズっとるやんけ。その節は温かく迎えて頂きありがとうございます。
さて、このアドベントカレンダーは、自分の日曜数学活動に関する記事を書くということで、Twitter でバズった数学の定理ランキング上位に入りそうな Riesz の表現定理とその活用について簡単に書きたいと思います。*1
Riesz の表現定理には様々な活用方法がありますが、私は特にその中で量子力学に用いられている bra-ket 記法を取り上げました。なぜ bra-ket 記法なのかについて、はじめに少しお話したいと思います。
関数解析と量子力学
「ヒルベルト空間と量子力学(新井朝雄著)」という本がたまたま家にありました。
「ええーっ。あの関数解析に登場するヒルベルト空間の、量子力学への応用があるのかい???」
マスオさんばりに驚いてまえがきを読んでみると、
量子力学の数学的基礎づけに関するフォン ノイマンの記念碑的な仕事以来、量子力学の数理に関わる研究は、関数解析学を数学的道具立ての中心に据える新しい数理物理学の潮流を引き起こし、今日に至っている。
とのこと。現在も研究の余地がまだまだある分野をまとめたものだそうですが、
量子力学の数学的枠組みを公理論的な形で提示
しており、数学が好きな自分にとってはとても興味深く、パラッと読んでみました。まだまだ研究途上の分野でしょうが、現象とヒルベルト空間の対応がとても綺麗で感動します。
自分は日頃数学カフェという勉強会をやっていて、数学関連分野の研究者の方のご講演+予習復習のセミナーのオーガナイズをしているのですが、一見かけ離れていると思われる分野にも関数解析に関連する様々な応用ないしは数学的基礎づけが登場しているため、その一つの応用例を学ぶのは(他分野への応用例との類似を考える上でも)面白そうだなと考えています。
さて、それでは少し詳細に入ってみましょう。
関数解析
そもそも、ここまででよく登場した関数解析とはどのような分野なのでしょうか?
宮寺功先生の著作の「関数解析」
のまえがきには、このように紹介されています。
古典的な解析学では、主として個々の関数や方程式の性質を取り扱ってきたのに対し、ここでは関数の集合である関数空間を考え、そこにおいて定義される作用素(関数空間の各要素に他の関数空間の要素を対応させる写像)の性質を位相的方法により研究し、解析学の理論を展開する。
とあります。*2
たとえば、(うまい設定をして)関数同士の和とスカラー倍を考えることで、ベクトル空間として関数の集まりを取り扱うなどのことをします。また、関数の微積分は古くから非常に重要な研究対象ですが、この微積分のような、関数に対して行われる操作も作用素とみなして、その性質がよく研究されています。(ここでは関数と書いていますが、関数以外についても同様の議論をすることも出来ます。説明を簡単にするため関数と書きました。)
ヒルベルト空間
先程、「関数同士の和とスカラー倍を考えることでベクトル空間として関数の集まりを取り扱う」と述べました。更に、このベクトル空間に、要素(ここではベクトル空間に含まれる元としての関数など)同士の内積を定義したものを内積空間といいます。ここで定義された内積を用いて、要素の大きさの一般化に相当するノルムを定めることができ、このノルムで完備になるときヒルベルト空間といいます。(完備がよく分からなくても今回は大丈夫で、なんかいい感じの内積空間なんだなと思って頂ければ。)
空間同士の包含関係はこんなふうになっています。
ヒルベルト空間 内積空間
ベクトル空間
ヒルベルト空間 の係数体(スカラー倍をする時にかけるもの)を K として、K 上のヒルベルト空間などと言います。特に K が実数のときは実ヒルベルト空間、複素数のときは複素ヒルベルト空間といいます。
ヒルベルト空間上の作用素
一般に、ベクトル空間 H のある部分空間 D からベクトル空間 K への写像で線形性を満たすものを H から K への線形作用素といい、これをTとおきます。またこのとき D を T の定義域といい、D(T) と表すこととします。
さて、,
をヒルベルト空間、Tを
から
への線形作用素とします。(ヒルベルト空間はベクトル空間です。)
定数が存在して、Tの定義域
に属するすべての元
に対して
<=C
が成り立つとき、T は有界であるといいます。(Tは線形なので有界線形作用素になります。)
を K 上のヒルベルト空間とし、
の部分集合から K への写像を汎関数といい、
から K への有界線形作用素を特に有界線形汎関数といいます。(このとき、係数体 K をヒルベルト空間とみなしています。)
双対空間
全体を定義域とする有界線形汎関数の全てからなる集合を
の双対空間といい
と書くとします。この集合は有界線形汎関数同士の和とKを係数体としたスカラー倍に関して K 上のベクトル空間となります。

気づいたのですが、ペンパイナッポーアッポーペンと有界線形汎関数で踏める。
自己共役作用素
,
: ヒルベルト空間、
T を
から
への稠密に定義された作用素とする。このとき、この T に対して以下を満たすものを
とする。ただし D(T) を T の定義域とする。
[tex: D(T*) := {\psi \in \mathscr{K}|すべての \phi \in D(T)に対して (\psi, T\phi){\mathscr{K}}=(\eta, \phi){\mathscr{H}} が成り立つような が存在する}]
ただし、[tex: (u, v)_H] はヒルベルト空間 H に定義されている内積のもとでの、[tex: u, v \in H] 同士の内積を表すとします。
このような D(T) は の部分空間であり、対応
はD(T)から
への写像を定めるので T は
から
の作用素となる。(これは線形。)T を T の共役作用素という。
ヒルベルト空間 から同じく
への稠密に定義された作用素 T について以下を満たすとき、Tは自己共役作用素という。すなわち、
すべての
に対して
は実数(これだけを満たすときTは対称作用素という)
D(T) = D(T*)
(すみません、時間がなくて解説の図をつけられませんでした…。)
Riesz の表現定理
Riesz の表現定理の主張は以下の通りです。

ケーキの仕様書は以下の通り。

この定理の証明はここでは割愛しますが、簡単に言うと、
をヒルベルト空間、
をその双対空間とすると、各
の元に対して、
[tex: \phi{F} \in \mathscr{H}] がただ一つ存在して、[tex: F(\psi)=(\phi{F}, \psi), \psi \in \mathscr{H}] と表され、さらに、
ということです。このような から
への同型対応によってこの2つを同一視して、
の共役空間
は
と等しい、ということもあります。
関数解析の話はまだまだ沢山あるのですが、Riesz の表現定理をご紹介するに留め、量子力学における bra-ket 記法に移ります。
量子力学
物理の方は関数解析に比較すると殆ど勉強していないので、ここで紹介するのは非常に恐縮なのですが、もし誤りがありましたらお教えください。
において
"量子力学"とは、物質と光の性質を詳細に記述し、特に原始的なスケールにおける現象を記述するもの。
と述べています。電子の挙動を調べる際には、現状で制約があり、たとえば、
"電子がどちらの孔を通り抜けたかを識別すると同時に、その干渉模様を壊してしまうほどには電子を撹乱することのない装置を設計することは不可能"
という制約など、2つ以上の物理量が同時に確定している状態になることはない、ということです。ハイゼンベルグらは、このような人間の実験的能力の限界に関する不確定性原理を提唱しました。実験技術の進歩の後もこの原理の正しさは破られていないそうです。*3
微視的なスケールの現象においては、上記が示すとおり、観測による系の撹乱の寄与が非常に重要になります。(巨視的な系の状態は観測の影響を受けないか無視することができます。)そのため、系の状態と観測可能量(物理量)の2つの観点で捉えることが重要です。この点が古典物理学と量子力学の大きな違いとなっています。
状態と観測可能量(物理量)
量子論の基本的仮定と枠組み
量子論では以下のように(実験結果に基づく)仮定を置いて理論の枠組みを構築します。ここでは、参考書籍に基づき物理量とは観測可能な量を指すとします。
すべての物理量が各瞬間に決まった値を持つことはない。
物理量 A の測定とは、観測者が測定値を一つ得る行為である。得られる測定値 a の値は同じ物理状態について測定しても一般には測定の都度ばらつくが、その確率分布 {P(a)} は A と
から一意的に定まるものとする。
任意の物理量の測定値の確率分布を与えるものを物理状態とする。すなわち物理状態
とは、各物理量 A から観測値の確率分布 {P(a)} への写像である。(以下、単に状態と書く。)
系が時間発展するとは、測定を行った時刻によって異なる {P(a)} が得られることを指す。*5
更に、いくつかの実験的事実から、状態の集合はヒルベルト空間とみなすことができ、物理量はこのヒルベルト空間上の自己共役作用素であると考えることでとても良い性質を導くことが出来ます(物理量を表す作用素の固有値が実数になるなど)。(そうでないような量子系を考えることも出来ます。)
少し混乱したので、以下のように図にまとめてみました。(誤りがあればぜひ教えて下さい!)

量子力学においては、状態を表すベクトル*6を Dirac が導入した bra-ket 記法と呼ばれる方法で表します。
を状態とすると、このベクトルは ket 記号を用いて
と表されます。
この状態に対して与えられる作用を行列
とすると状態への作用は
また別の状態
との内積を計算する操作を表す bra 記号というものを用いて <φ|ψ> と表されます。
と
はどちらも状態であるはずですが、なぜわざわざ、片方だけを状態と決めて ket で表し、もう一つのほうを内積を作るという操作として bra で表すのでしょうか?
Amazon 探索で取材班が見たもの
その謎を探るため、我々取材班は Amazon.com で検索して買った色んな本を読み漁って考えました。
ファインマンの物理学(量子力学)の方を読んでいると、<観測後の状態|A(何らかの観測)観測前の状態>という説明がなされていました。歴史的経緯についての調査がまだ十分でなく、ここにおいてファインマンは演算子形式の量子力学の立場をとってこの記号を用いているのかは定かではありません。(演算子の章は第20章と最後の最後の方に補足的に書かれており、現代の表記の意義との対応を確認していません。)しかし、少なくともファインマンは上記のように bra-ket 記法を用いて、観測前と観測後の状態を明示的に分ける意図が込められていたということがわかります。さらに、状態に物理量を作用させて新しい状態を得る式 だけでも意味のあるものにはなるが、この式は、<x| のようなbra を作用させることによって初めて実数値 <x|
|ψ> が得られて完成される、"未完"のものであることを示す意図もあると示唆されています。(p.139)
上記のことから、(繰り返しになりますが)2つの状態の内積を取る操作を bra-ket 記法を用いて考えるにしても、観測前後であることをそれぞれ明示する意図と、観測前→何らかの物理量(&観測)→観測後の状態のどこの段階にあるかを明示する意図があったのではないかと今の所考えています。
さて、では、観測前の状態→観測後の状態の違いを明示したいという意図でこの記法を採用しているとここでは仮に認めるとして、(観測後の)状態であるはずのものを「内積を取るという操作」に変えてしまっても本当に良いのでしょうか??(状態と内積を取る操作の間には1:1の対応が取れているのでしょうか。)内積を取る、という操作は状態とは異なるもののはずです。またその後、ブラとケットを適当に入れ替えて多くの関係式を得ていますがこのような入れ替えはwell-definedなのでしょうか。
さて、実は、ここに Riesz の表現定理の具体例が出現しています。
Riesz の表現定理の主張を振り返ってみます。
 しつこいか。
しつこいか。
をヒルベルト空間、
をその双対空間とすると、各
の元に対して、
[tex: \phi{F} \in \mathscr{H}] がただ一つ存在して、[tex: F(\psi)=(\phi{F}, \psi), \psi \in \mathscr{H}] と表され、さらに、
(すみません、ここもちょっと今時間がないので後ほど直します…。)
ここで一旦簡単のため、状態のなすヒルベルト空間を有限次元であるとします。
突然のFact 有限次元のヒルベルト空間 H から有限次元のヒルベルト空間 K への線形作用素は有界。
つまり、このとき、状態のベクトルに対して、ある(ここでは状態のベクトルとは呼ばない) bra 記法で表される操作を施し内積を得る写像は有界線形汎関数であるとみなせるため、その bra 記法から一意に状態のベクトルを定めてその2つのベクトルの内積を取るという操作と同一視できる、ということが Riesz の表現定理から保証されます。
無限次元の場合は、線形であるということだけからは有界性は導けず、コーシー・シュワルツを使うと良さそう…だけどまだ証明出来ていない、おおどうしようと思ったところで締め切りである16日の朝(9時)を迎えてしまいました…。もう月曜数学じゃないか。無限次元の場合については今後の課題としたいと思います。
勉強していたことが意外なところで登場すると面白いですね!これからも日曜数学を続けたいと思います。
参考文献
上に載っていない参考文献としては、次のものがあります。ご参考になりましたら幸いです。
また、新装 量子論の基礎は結婚披露宴の時に数学仲間の方にプレゼントして頂きました!とてもいい本で、細かい注意書きも勉強になることばかりでしたので本当に嬉しいです!ありがとうございます。
明日のアドベントカレンダーは微分加群がテーマだそうです。楽しみです!
*1:披露宴は土曜日でしたが、日曜数学会あるある(土曜日に開催)ですね。
*2:新井仁之先生によるこの本の解説も、今後勉強する上でとても参考になり、面白いのでもしよければ御覧ください。www.webchikuma.jp
*3:不確定性原理は様々な研究者が様々な実験に基づき提唱していますが詳細は量子論の基礎を御覧ください。
*4:ここでは、演算子形式の量子力学の中でもシュレディンガー描像と呼ばれる形式を採用するものとします。
*5:{P(a)} は A と によって定まりますが、Aが時間変化せず
が時間変化すると考えて時間発展を定式化したものをシュレディンガー描像といい、今回はこの立場を採用します。
あなたの街でも数学カフェを開いてみませんか?〜数学カフェ開催の tips 〜
先日、数学カフェ 確率・統計・機械学習回を開催し、なんと117名の方に来ていただきました!
数学カフェとは、
- 誰でも気軽に、深く数学を学べるようにしたい
- 様々な分野の人と数学を軸にして交流し、創造的な活動が出来るようにしたい
- 数学者が、専門外の人に伝えることが出来る場になるようにしたい
という理念のもと、およそ月1で開催しているイベントで、 各分野の専門家や愛好者を講師にお呼びし、 たとえば素数だけで6時間話し通したりするというものです。 (文系の方や、1歳半の赤ちゃんのご参加もありましたね!)
前回の活動報告はこちら:
mathcafe-japan.hatenadiary.com
参加者の方から、なんと、
「自分の街でも数学カフェを実施したいのでテンプレを教えてください!」
と言っていただきました! 嬉しいです!ありがとうございます!!!!
以前にも、勉強会を継続するためのtipsという記事を書きました。
今回はそちらに書いていない項目について書いていこうと思います。 と言っても私も色々試行錯誤中ですが…。
それでは、どうぞお付き合いくださいませ。
目次
宣伝の仕方
宣伝媒体についての考察
不完全なところもありますが、告知の際の検討事項を昔ざっくりまとめました。こちらを御覧ください。
www.slideshare.net
告知文の書き方
告知文は毎回、講師の方にほぼお任せしていますが、一応少しだけ気をつけていることがあります。 (気にしない時もあります。突っ走ると面白いと思ってくれる人が集まる時がある。)
- 対象者を明らかにすること
- その対象者は何を魅力的だと思うのか考え、明示すること
- 要点を強調すること
たとえば前回の数学カフェでは、こちらのサイトに掲載されている通りになりました。
文章のボリュームがあったので、対象者と要点にアンダーラインを引き、目に留まりやすくしました。 (この要点の部分は、事前に何を特に伝えたいか話し合って決めた箇所でもあり、事前の打ち合わせが大事だと思います。)
ちなみに、このconnpassという告知サイトは
- SNS機能もあり
- エンジニアの方に多く使われており
なかなか重宝しています。
良い講師の方の探し方
私が一番大事にしているのは、良い講師の方に来ていただくことです。いい人を見つけたら、直ちに声を掛けます。(言い方w) もちろん、周りの方々からのご推薦を頂くのはとってもいい方法です!
加えて、私が思ういい先生の選び方は、(当然ながら?!その分野について深い見識のある方ではありますが)何より、優しい人です。聞く人の目線に立って考えられる人。他人のこと、他分野の人のことを簡単に見下さない人。 特に、数学を学んでいない人にも来ていただきたいので、必須です。 一緒にお仕事をさせて頂く中で、いつも多方面から様々な学びを得ています。
あと、まだまだ不勉強なのですが、いい講師の方に来ていただくために、ほんの入り口でしかなくても、自分もその分野を勉強することを心がけています。深く学びたいのです!!!という思いを行動で伝えるようにしていますし、構成を考える上でもとても役に立つと思います。
素晴らしい講師の皆様に支えられて、数学カフェを開くことができています。ありがとうございます!
簡単ではありますが、以上です。お役に立てば幸いです。 読んでくださりありがとうございました!また思いつくことがあればまとめてみます。
勉強会を継続するための tips
こんにちは。はるさんです。
色々切羽詰まっています。
切羽詰まっているときは掃除が捗ると言いますが、
仕事の仕方について振り返ろうということで、
勉強会継続ためのコツをまとめてみました。
今まで、1年半ほど数学カフェなる勉強会を開いていまして、
これまで16回開催し、
最近だと大体70名くらいの規模になってきました。
数学カフェのfacebookページ:
https://www.facebook.com/mathcafejapan/
どれぐらいの人数が望ましいかは色々な考えがありますが、
数学カフェの場合は
1日かけて、数学の一分野の概観をつかむことを目標にして
その分野を専門に研究されている方を講師にお呼びしています。
いい講師の方をコンスタントにお呼びするためにも、
これくらいの規模がちょうどいいのかなぁと思っている次第です。
継続のために必要なことの全体像としては以下のような感じ。
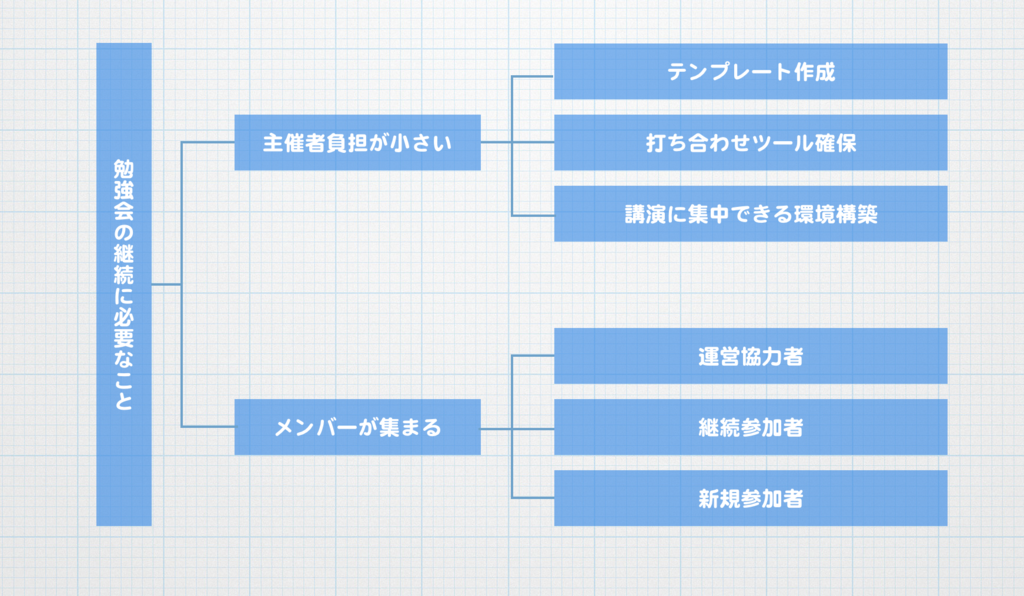
主催者の負担を極限まで下げながら
継続的にメンバーを集めることができれば、
勉強会は継続できるのかなと。
(ただ、継続は目的ではなくて手段であって、
あくまで自分にとって意味のあるものであるという前提がありますが。)
それぞれ個別に、今大事だなぁと思うことをまとめます。
主催者負担が小さい
負担大きいと続かないし、本業を圧迫していては本末転倒です。。
というわけで、
今、開催にかかる時間を少なくするべく頑張っています。
こんな風にして減らせるのではないかなぁというコツをまとめてみます。
テンプレートの作成
できるだけ同じ作業はテンプレを作って、
作業の重複がないようにします。
テンプレとは、文面のテンプレートだけではなく、
開催の方法なども含みます。
このテンプレは、適宜良いものが見つかり次第、改善します。
(オブジェクト指向プログラミングを学んだ方はイメージしやすいかも。)
どんなところをテンプレ化したら良いか、書いてみます。
1. 開催方法
- 会場は同じところにする
- 基本的なタイムテーブルを同じにする
- 呼びかけツールを統一する
- 開催スケジュールを統一する(毎月◯日に告知、など。)
- 準備のときに必要な項目・物品・todoをまとめておく
- 参加者の行動・性格パターンを理解する(笑)
マンネリ化する恐れもありますが、
その分学ぶ中身の工夫に集中できます!
同じところを利用していると信頼関係も築けますし、安心です。
最後の、参加者の行動・性格パターンは半分冗談もあるけれど(笑)
でも半分はかなり真剣です。
◯◯さんは早めに前もって連絡をしたほうがいいな、
何時頃だったらすぐにレスポンスが来るかな、
facebook で連絡するより twitter の方が返事が早いな、
などの傾向が掴めていると、スケジュールも無理なく進められますし、
精神衛生上楽ですし、精神衛生上楽です。
返事を待つ間は頭のなかにも残っちゃいますしね。
2. 案内文
- 活動内容紹介文(講師の依頼などの説明に)
- 告知文の内容
- 活動報告
後輩の方に伝える場合には、このテンプレを伝えるようにすると楽かも。
こまめにまとめると、良いことあるんですね。
打ち合わせツール確保
人との打ち合わせもなかなかタイムラグや負担が発生するところなので
これもいいツールを使えるといいですよね。
数学カフェでは今、Slackを活用しております。
Slackは、項目ごとに話し合いが出来る場所(チャネル)を作ることができたり、
ファイルのシェアや、ビデオチャットなどができたりするツールです。
詳細はここが詳しいかな。
毎回どんな項目が必要か決まっているので、
作成するチャネルとその説明文もテンプレ化しています。
たとえば、
#PR
#contents
#schedule
#todo
など。
使いこなすととっても便利なので手放せません・・・!
講義に集中できる環境
自分が運営する側になると、当日はバタバタして話が聞けない・・・
なんてことがあったりします。
これって相当なモチベーションダウンです・・・。
ということで、当日運営の人が勉強に集中できる仕組みを作ることが
とっても大事だと考えました。
最近は、受付完了した人に名札(ネームシール)を配り、
遅れてきた人には休み時間に受付をしてもらうことに。
講義中には気を逸らさないように工夫しています。
あと、その後の二次会をする場合、
参加人数の変動は金額的にも大きなリスクで、
講義中も気が休まらなかったりします。
(2回、結構たいへんな気持ちになった。)
急な変更にも対応していただけるところ
を探して、常連さんになるのがよいと思います。
メンバーが集まる
一般的にメンバーが集まるために必要なのは、
内容について関心があり、満足できること。
人が集まるのが勉強会をする上では一番大事ですよね。
基本的には、相手が持つ希望をよく理解するように努めて、
この勉強会でそれが達成されることを実感してもらうのが大事だと思います。
この項目については、
会の性質にも大きく依存すると思うので、少しだけ。
数学カフェの場合についてはまた別の機会に詳しく書こうと思います。
運営協力者
一緒に運営をして頂く場合、
よくコミュニケーションを取ることがとても大事ですよね。
人間関係が原因で空中分解してしまう話、
たまに聞きます。
こういう人間関係であるべき、というのはなくて、
それぞれ、気が合う人同士で集まればよいと思うけれど、
会についてどんな期待をしているのか、
互いにどんな要望があるのか、
気分良く話し合える環境づくりがとても大事だと感じます。
みんなそれぞれ得意分野があると思うので、
組み合わせて、力を発揮できたらいいなぁと思っています。
その他、運営をすることでどんな経験が出来るのか、
自分自身でも一度言語化すると、
協力をお願いするときにお願いしやすいかもしれません。
継続参加者
継続参加者を増やすためには、会の満足度を上げることが大切です。
このためには、事前の期待と、経験後のマイナスなギャップがないこと、
期待を上回る楽しさや収穫があることが大事ですね。
事前の期待とのミスマッチを避けるためは、
告知を丁寧に考えることが大事ですね。
- どんな前提知識が必要なのか
- 雰囲気やレベルを適切に伝えられているか
などを押さえておくとよいでしょうか。
期待を上回る楽しさについては、
- 内容的に得るものが大きい
- 参加者同士、出会えてよかったなと思えること、
などなど、色んなポイントがあります。
この辺については更に長くなるので、またの機会に。
ちなみに数学カフェは、度々聴衆置いてきぼりになることもあると思うのですが、
1日で理解できることは広い分野のなかのほんのわずかですし、
だからこそ、この機会に『もっと勉強したい!!!!』という想いが湧くような
勉強会にしたいという思いを伝えるようにしています。
新規参加者
新規参加者を増やすためにはどうしたら良いのだろう?
そもそもそれは必要なのか?
勉強会の目的や内容によりますよね。
一冊の本を通読するような勉強会の場合は、
新規参加者がいても、キャッチアップ出来なくて困るかも知れません。
新規参加者が必要である場合としては、
- オムニバス形式の勉強会
- 後輩さんたちに引き継いでほしいような勉強会
が挙げられます。
他分野を幅広く学びたい勉強会の場合、
ひとつの回に興味があっても別の回には興味が無いかもしれない。
方法としては、既に来てくださっている方に満足していただくとか、
あるいは、『この話聞きたい!!!』と思ってもらえるような告知文をつくるとか。
これもまた、別の機会に話したいなぁと思います。
そんな感じで、ちょっと尻切れトンボで恐縮ですが、
今工夫していることをまとめてみました。
やりくり、がんばるぞい。
はじめまして。
最近、論理的な長文をあまり書かないので
頭の衰えを感じるこの頃です。
周りの皆さんを見習って、
- わかりやすく
- 論理的に
文章を書く習慣をつけようと考えて、
ブログをつけ始めることにしました。
継続的にブログを書くことには、次のようなとてもいい効果があると感じています。
- 内容のある投稿をしようとすることで、深く学ぶ習慣がつく
- 多量の情報をまとめることで、長文を構造化して書く能力が身につく
- 伝える相手を意識することで、さらなる内容の理解に繋がる
また、上記を繰り返すことで、アウトプットのスピードも上がると考えられます。
日頃あまりアウトプットの習慣がない自分ですが、
ここで喝を入れて、さらなるレベルアップのために
ブログに挑戦していこうと思います。
内容は様々なトピックに渡ると思いますが
基本的には数学について書く予定です。
- 面白い数理モデルの紹介
- 純粋数学の話
- その他サイエンスにまつわること
- 人間関係について思うこと
- 心のあり方について
などなどが主な内容になると思います。
どうぞよろしくお願いいたします。





